Exposición «El Rostro Humano de las Matemáticas»
Esta exposición nos fue cedida por la Real Sociedad Matemática Española para que pudiéramos disfrutar de ella durante el ENEM. Como recordaréis, estuvo expuesta en los pasillos de la Facultad de Ciencias. El Rostro Humano de las Matématicas
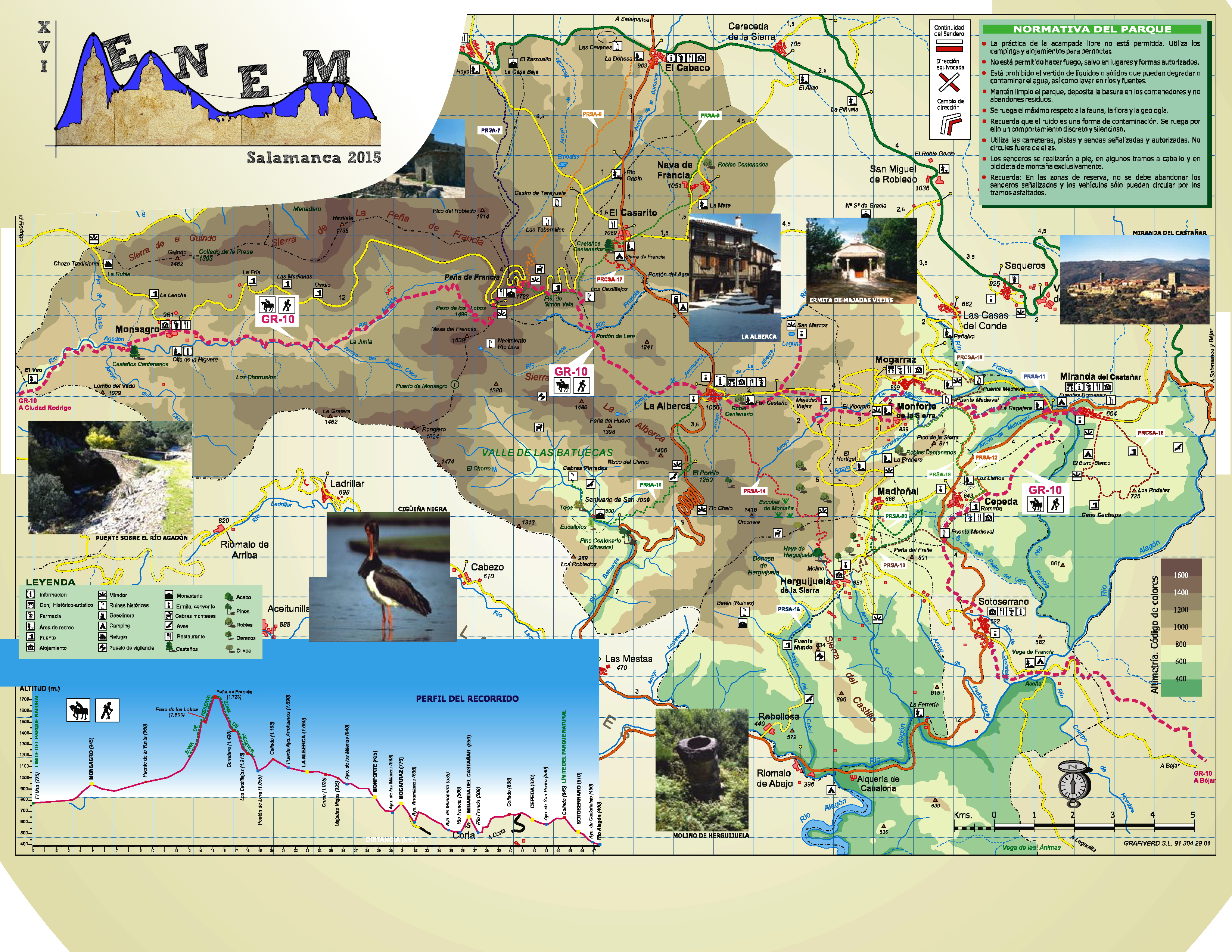
La Alberca. Información
La Alberca, Conjunto Histórico, Rutas e instalaciones de uso público
Enigmas diarios. Respuestas ganadoras
Engima 1, lunes 27 de julio
«Lo primero que se nos ocurre es una relación tipo triángulo de tartaglia y al ver que en la base del triángulo aparecen dos números que distan dos unidades y comparten el segundo numero observamos los del tercer nivel relacionados con los anteriores. Vemos que distan también dos unidades luego la relación es lineal. Basta ver que es la suma de los del nivel inferior multiplicados por algo menos otro algo. Probando vemos que es simplemente la suma y restar quince luego D=1345 y E=2440.»
Roberto Giménez Conejero
Engima 2, martes 28 de julio
«Curiosidades del lenguaje, ¿verdad? El que una palabra tenga varios significados, polisemia, unido a la homonimia, puede acarrear situaciones divertidas. Por ejemplo, el siguiente razonamiento:
Premisa 1: Todo sujeto que produce un corte a otro es maleante.
Premisa 2: Todo cirujano produce cortes a otros sujetos.
Conclusión: Todo cirujano es maleante.
Esto se puede extender un poco más, como veréis en los siguientes chistes, si es que se pueden llamar así:
-¡Almirante, quince carabelas aproximándose!
-¿Una flota?
-No, flotan las quince.
Una señora en un restaurante:
– ¿Me da usted un pollo?
– Con salsa…
– ¡Un poooolllllitoooo para gossssaaarrrrrr!!
Bueno, pues vayamos ya a lo que teníamos planeado, el problema del martes. Tan solo hemos de formar un 4, nada más. Solo que de la forma que nos lo enseñan en la escuela. Cogemos el «palo» de la derecha, lo giramos hasta que sea vertical, y lo ponemos al final del palo izquierdo, sobre el mismo, de forma que obtenemos el grafo. Con solo recordad que 4 es dos la cuadrado, hemos movido un palo para formar un cuadrado, aunque no como el que pensamos en primera instancia, de ahí lo previo.»
Andrés Mateo Piñol
Como curiosidad:
«Supongamos que tenemos 4 segmentos (gordos, con área) iguales. Puesto que los segmentos no deben solaparse (supongamos SPG que son cerillas) el área del centro de la figura es debida a que uno de los segmentos está dentro del hueco que dejan los otros tres. Por tanto, basta con desplazar el segmento que cubre el hueco tanto como su anchura y colocarlo en una posición simétrica con los otros tres. Quiere decirse, la posición final que deja un cuadrado en el centro es tal que,fijado un segmento, cualquiera de los demás se puede obtener vía una isometría (o un movimiento, si el lector considera más oportuno pensar que la pantalla del móvil por el que estoy escribiendo en una discoteca salmantina se asemeja más a un espacio afín que a uno vectorial).»
Jorge Becerra Garrido
Enigma 3, miércoles 29 de julio
«Pues hay varias opciones:
- Suponiendo que todos los coches son iguales (en cuanto a mecánica se refiere, para que la carrera sea justa) bastaría con que cada conductor cogiera un coche que no es el suyo, de tal forma que todos los conductores se esforzaran para llegar primeros a la meta con el objetivo de que el propietario del coche que cada uno conduce pierda, de esta forma la carrera se llevaría a cabo de forma normal.
- En el caso de que hubiera diferencias en la mecánica del coche, debiera darse un tiempo de ventaja extra a los coches con menos potencia, realizando el estudio correspondiente para que todos los coches tengan la misma probabilidad de llegar primeros independientemente de su potencia.
-Por último en el caso de que el circuito tuviera longitud infinita, nos daría igual en que posición partiera cada coche, ya que al llevar una velocidad finita sería imposible que acabaran la carrera, además de las limitaciones de velocidad habría que tener en cuenta las fisiológicas ( sueño, hambre, urinarias y de desecho, aunque estas últimas tendrían fácil solución con un pañal de adultos, pues suponemos que todos los conductores tienen la edad adecuada para la conducción de vehículos).»
Jesús Martín Ovejero
Enigma 4, jueves 30 de julio
«La respuesta es 14123113.
Explicación: es una sucesión por recurrencia. Supongamos que queremos saber el término a_n de la sucesión. Para ello tenemos que mirar el término a_{n-1} y ver sus cifras apuntando cuántas veces aparece cada una de ellas. Vamos a verlo con dos términos ya calculados de la sucesión: por ejemplo, si a_{n-1} = 1211, entonces sale 3 veces la cifra 1 y 1 vez la cifra 2, por lo que tendremos los pares 3-1 y 1-2 por lo que el término a_n será 3112. (Nota: el término a_n es 3112 y no es 1231 porque el orden de los pares es el orden en el que aparecen las cifras en a_{n-1}).
Por tanto, como el último término dado en la sucesión del enunciado es 421311, tendremos los pares 1-4, 1-2, 3-1, 1-3 y por tanto el nuevo término será 14123113.
Si seguimos la sucesión, los siguientes términos a este serán 41141223, 24312213, 32142321, 23322114, 32232114, etc.»
Eva María Alarcón Díaz y David Iglesias López
Enigma 5, viernes 31 de julio
«20:
-9 de 1×1 (obvio)
-4 de 2×2 (evidente)
-1 de 3×3 (ejercicio)
-4 cuadrados diagonales de sqrt(2) x sqrt(2) (uno de ellos es el que tiene como vértices los puntos, en coordenadas cartesianas, (1,2),(2,1),(3,2),(2,3).
-2 cuadrados de sqrt(10) x sqrt(10) (por Th Pitagoras) (uno de ellos es el que tiene como vértices (2,1),(1,3),(4,2),(3,4).»
Jorge Becerra Garrido
Concurso de fotografía. Fotografías ganadoras
Primer premio: Devorado por la geometría proyectiva, de @irisfosforito, @dgonzalezmoro y @bobisnay.
Segundo premio: MATHS&MAGIC, de @AlmuDokiie.
Tercer premio: Proporción Áurea, de @Im_a_Soulman.
El título del libro que se les dio a los ganadores es El azar no existe, de Jesús López Fidalgo, al que agradecemos su aportación. El libro se puede adquirir siguiendo este enlace: El azar no existe.
Fotografías graciosas:
Arruga geodésica, de @JcVirin.
Unión de Venus, de @juanripu.
El grafitero con nombre de sumatorio, de @TovRodero.
Casino del Tormes. Información